1) 행렬(Matrix)
row와 column을 기준으로 하는 단순한 수의 배열. 따라서 element가 하나여도 matrix 그 자체.
행렬은 통상적으로 알파벳 대문자로 표현, 성분은 소문자로. 보통 row와 column을 m x n 으로 명시.
- 영행렬(zero matrix)
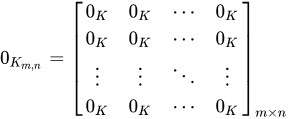
- n차 정사각행렬(n-square matrix)

- 주대각원소(main diagonal element)
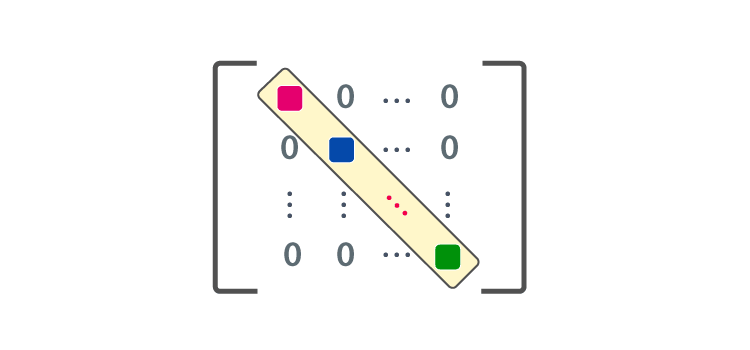
- 항등행렬(unit matrix : I)
주대각원소의 값만 1이고, 나머지 모든 원소들이 0인 정사각행렬. 곱셈에서의 항등원인 0과 같은 역할을 함.
2) 행렬의 연산
덧셈과 뺄셈은 두 matrix의 크기가 같아야 함.
곱셈에는 행렬에 실수배를 하는 스칼라곱과 행렬끼리의 곱으로 나뉨.
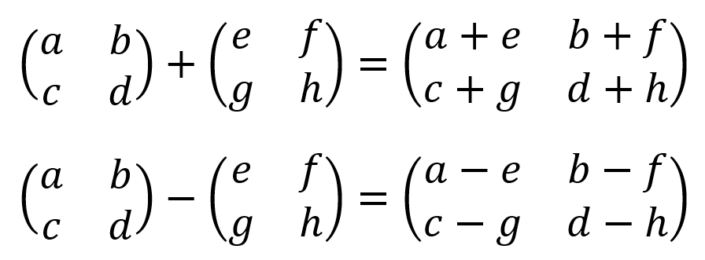
- 행렬의 스칼라곱(scalar multiplication)
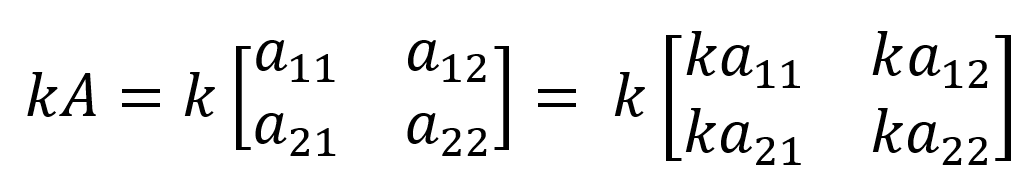
- 행렬끼리의 곱(matrix multiplication)

계산이 row x column이므로 결과값의 row와 column을 보면 순서가 헷갈리지 않음.
3) 행렬의 종류
- 대각행렬(diagonal matrix)
주대각원소를 제외한 나머지 원소들이 0인 행렬. 따라서 항등행렬도 당연히 포함됌.
- 전치행렬(transpose matrix)
row와 column을 바꾼 행렬. n x m matrix. 행렬표시 대문자 위에 T가 붙음.
- 대칭행렬(symmetric matrix)
정사각행렬 중 원본과 전치행렬이 일치할 때.
4) 기본행연산
선형대수는 결국 함수로 표현했을때 선을 그릴 수 있는 선형방정식을 푸는 것.
선형방정식을 푸는데 있어서 기본행연산을 통해 기존 행렬을 대체하는 것이 필수.
대체하는 것을 허용하는 것일뿐 일치하지 않음. " = " 는 틀린 표현 " -> " 가 올바른 표현.
