

from math import *
print(gcd(12,8))
print(gcd(66528,52920))

Extended Euclidean Algorithm
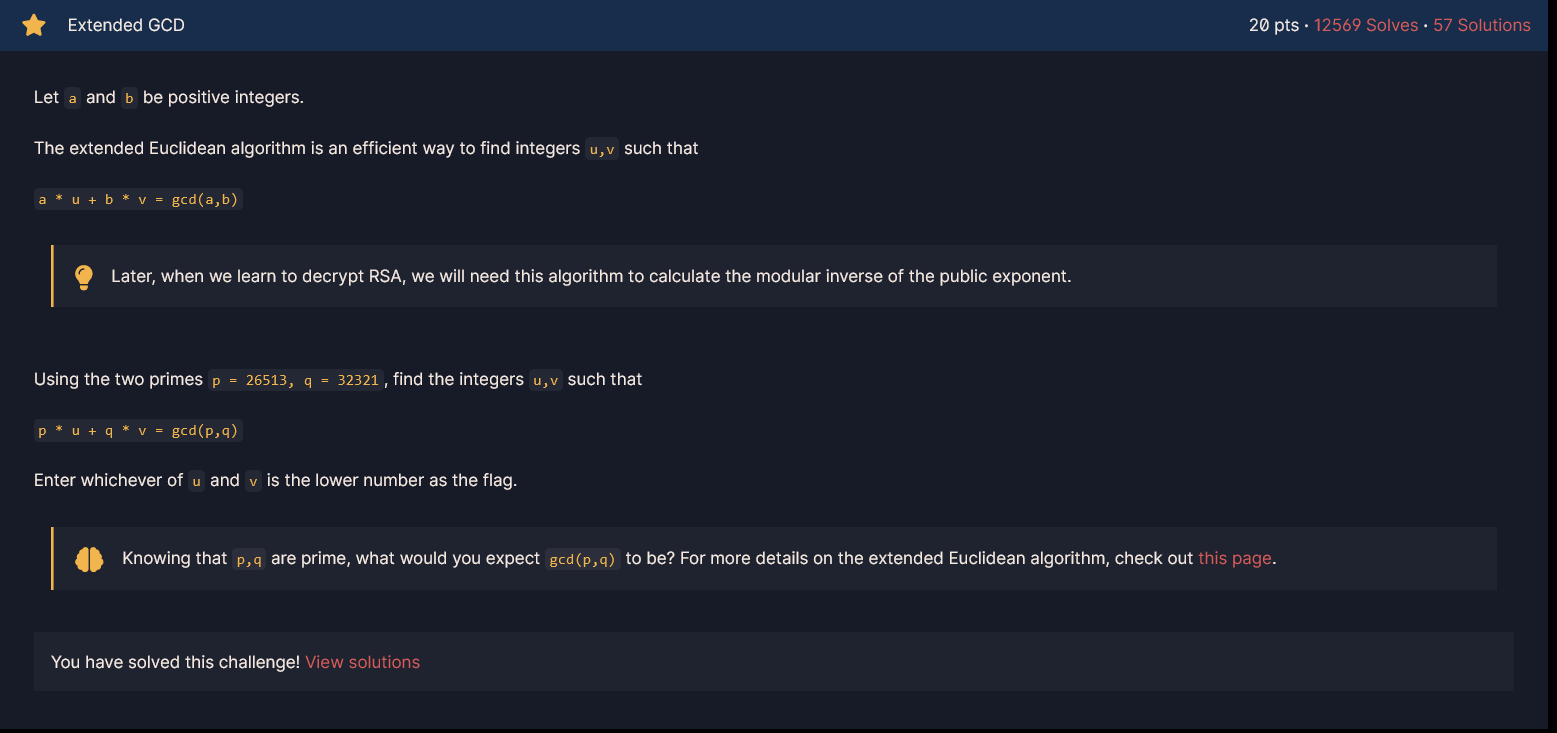
The Extended Euclidean Algorithm As we know from grade school, when we divide one integer by another (nonzero) integer we get an integer quotient (the "answer") plus a remainder (generally a rational number). For instance, 13/5 = 2 ("the quotient") + 3/5 (
web.archive.org
위의 문서에서는 유클리드 호제법과 확장 유클리드 호제법에 대해 설명하고 있습니다. 문서를 읽으면서 최대한 이해하기 위해 노력해봅니다.
def egcd(a, b):
if a == 0:
return b, 0, 1
gcd, x1, y1 = egcd(b % a, a)
x = y1 - (b//a) * x1
y = x1
return gcd, x, y
print(egcd(26513,32321))


print(8146798528947%17)


print(pow(273246787654,65536,65537))


q = 0
while (13*q+1)%3!=0:
q+=1
print((13*q+1)//3)

'security > crypto' 카테고리의 다른 글
| [Dreamhack] likeb64 풀이 (0) | 2023.12.17 |
|---|---|
| [Dreamhack] ICM2022 풀이 (0) | 2023.12.17 |
| [CryptoHack] Introduction to CryptoHack (2) (0) | 2023.11.22 |
| [CryptoHack] Introduction to CryptoHack (1) (0) | 2023.11.20 |
| [Dreamhack] Textbook-DSA 풀이 (0) | 2023.11.15 |

