[암호학 이론] DES 암호화 알고리즘

 

 

 

 

 

- DES(Data Encryption Standard)

 

DES algorithm (1)

 

DES 알고리즘은 위의 그림과 같이 초기 순열(Initial permutation), 총 16번의 라운드 함수, 그리고 최종 순열(Final permutation)의 과정으로 이루어져 있습니다. 또한 8바이트(64bit)를 한 블록으로 하는 블록 암호임을 그림을 보면 알 수 있습니다.

 

DES algorithm (2)

 

DES 알고리즘에서 라운드 함수를 적용하는 부분을 조금 더 자세히 보면 다음과 같이 페이스텔 구조로 이루어져 있음을 알 수 있습니다.

 

2023.11.01 - [crypto] - [암호학 이론] Feistel cipher

[암호학 이론] Feistel cipher

페이스텔 구조를 모르시는 분들은 앞에 작성했던 이 게시물을 읽고 오시면 이해하는데 도움이 되실거라 생각이 듭니다. DES 알고리즘의 전체적인 구조에 대해 간단하게 알아보았기 때문에 이제 DES 알고리즘의 과정을 자세히 설명 해보겠습니다.

 

 

 

- DES algorithm process

1. Initial permutation & Final permutation

2. Round function

 

 

 

1. Initial permutation & Final permutation

 

Initial permutation and Final permutation

 

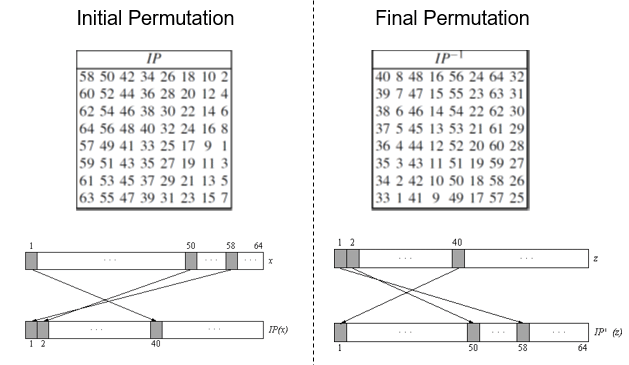
DES 과정에서 첫 단계인 초기순열(Initial permutation)은 암호화할 평문의 한 블록(64bit)을 비트 단위로 전치를 합니다. 예를 들어 58번째 비트값을 1번째로, 50번째 비트값을 2번째 등등 모든 비트값들의 순서를 바꿉니다. 이후 16번의 라운드 함수를 거쳐서 암호화된 블록을 마지막으로 최종순열(Final permutation)을 시행 합니다. 이때는 초기순열에서 순서를 바꾼 것들을 원상태로 복구를 해줘야 하므로 초기순열을 역으로 시행한다고 생각하시면 됩니다. 예를 들어 아까 58번째와 50번째 비트값들을 1번째, 2번째 비트값으로 전치했으므로 1번째, 2번째 비트값들을 58, 50번째로 다시 순서를 바꿔줍니다. 이와 같이 최종순열은 초기순열과 역의 관계에 있으므로 Inverse initial permutatioin, IP^(-1)이라고 부르기도 합니다. 위의 그림을 참고하시면 쉽게 이해하실 수 있습니다.

 

 

 

2. Round function

 

Round function

 

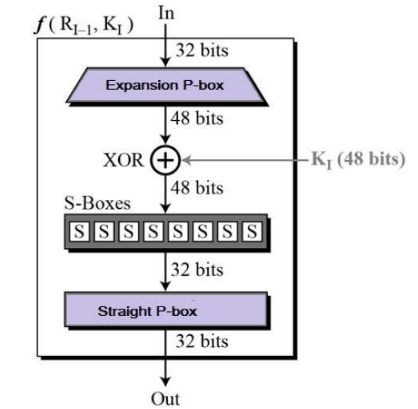
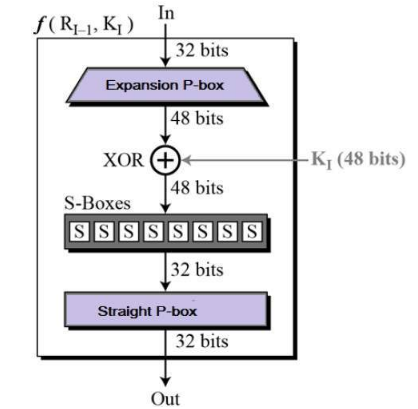
라운드 함수는 확장순열(Expansion P-box), 라운드 키와의 xor 연산, 치환 테이블(S-box), 고정 순열(Straight P-box)의 과정으로 이루어져 있습니다.

 

 

 

- Round function

2.1. Expansion P-box, Straight P-box

2.2. key xor

2.3. S-box

 

 

 

2.1. Expansion P-box, Straight P-box

 

P-box(Permutation box)

 

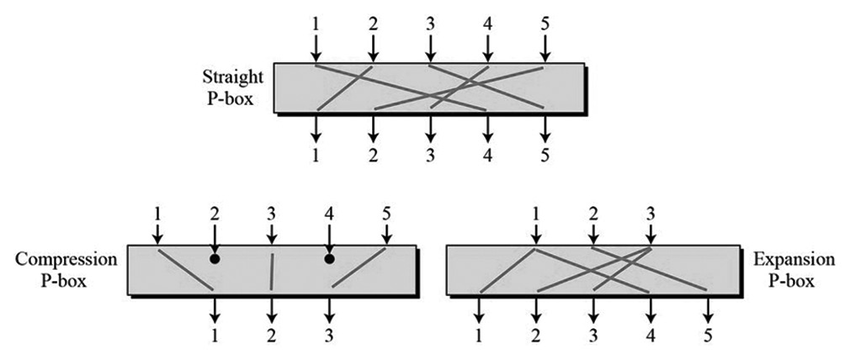
순열(Permutation)을 시행하는 상자를 P-box라고 부르는것 같습니다. 순열은 위에서 알아보았던 초기순열과 최종순열과 같이 값들을 전치시켜준다고 생각하시면 됩니다. P-box에는 크게 위의 그림과 같이 세 종류가 있습니다. P-box의 시행 전과 후에 값의 갯수의 변화가 없는것은 단순순열(Straight P-box)만이며, 축소순열(Compression P-box)와 확장순열(Expansion P-box)에는 이름과 같은 변화들이 보입니다. 복호화 과정에서 암호화 축소순열 때 빠진 값들을 알 수 없으며 확장순열 때 추가된 값을 알아내지는 못한다는 특징이 있습니다.

 

DES Expansion P-box

 

 

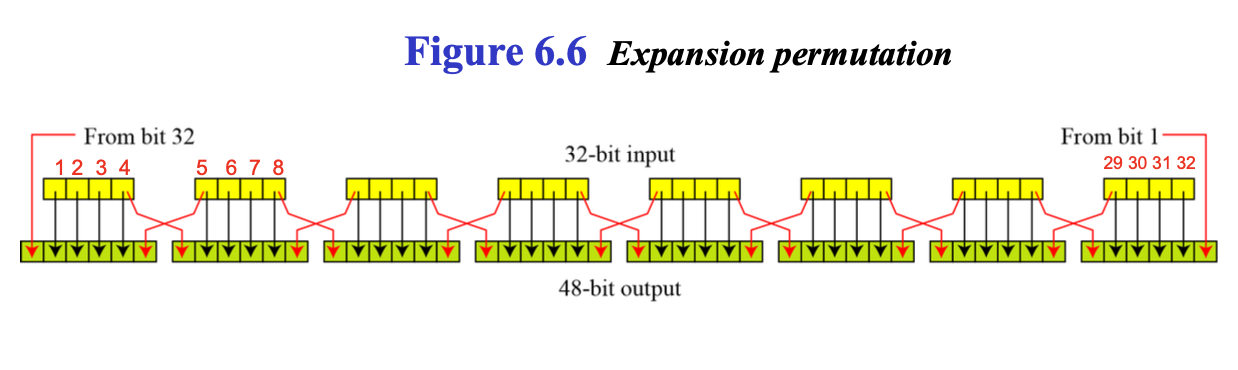
라운드 함수 속 확장순열의 자세한 방식은 위의 그림과 같습니다. 위의 방식으로 입력받은 32비트를 48비트로 출력합니다. 비트들을 더 보기 쉽게 표로 정리하면 밑의 그림과 같습니다.

 

DES Expansion P-box table

 

 

 

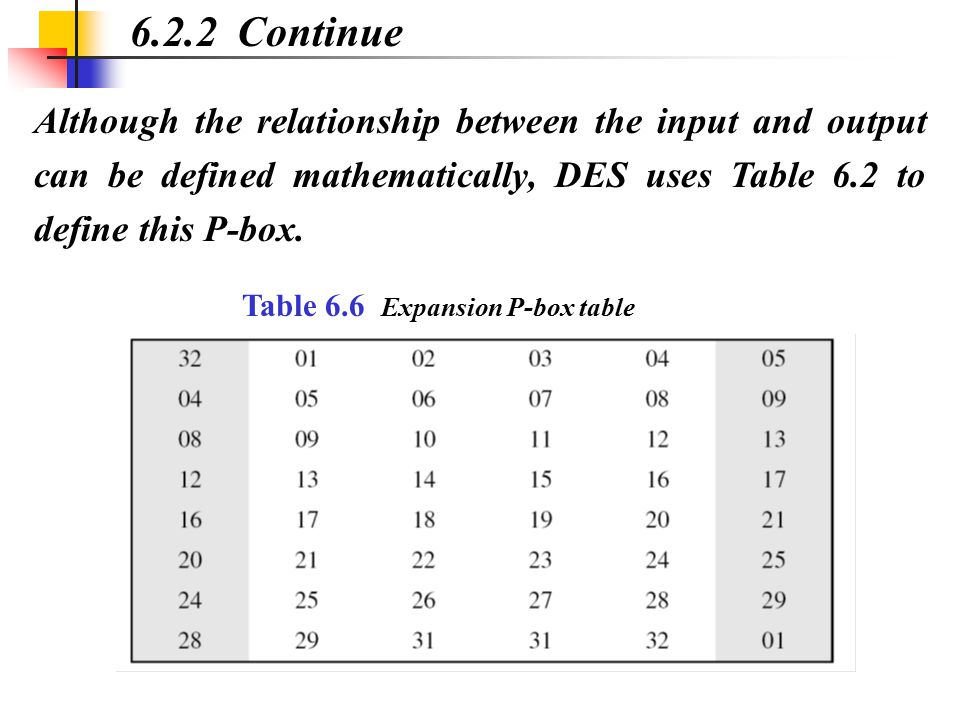
2.2. key xor

 

각 라운드마다 확장순열(Expansion P-box)를 거친 값과 xor 연산을 할 키 값이 생성됩니다. 확장순열을 거치면 48비트가 되므로 키 값도 48비트로 생성해줍니다. 키 생성함수의 과정에 대해 알아보겠습니다.

 

Key scheduling

 

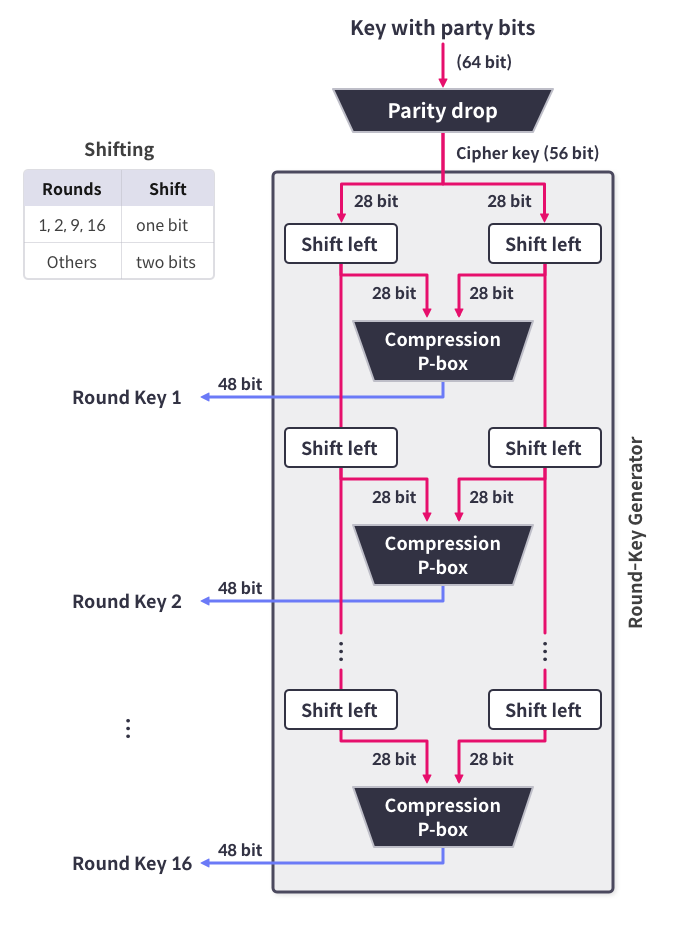
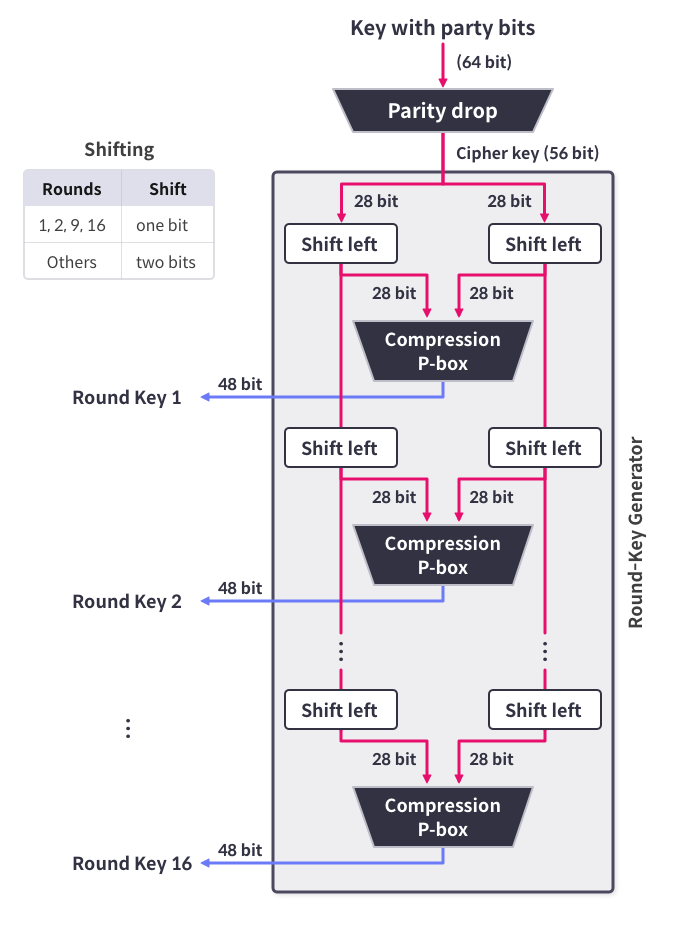
키 생성함수는 위의 그림과 같이 패리티 비트 제거(Parity drop), 쉬프트(Shift), 축소순열(Compression P-box)의 과정으로 구성되어 있습니다.

 

 

 

- Key scheduling

2.2.1. Parity drop

2.2.2. Shift

2.2.3. Compression P-box

 

 

 

2.2.1. Parity drop

 

Parity bit

 

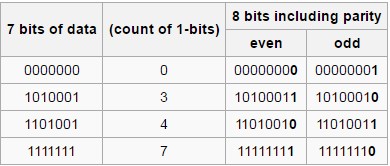
패리티 비트(Parity bit)는 전달 받은 정보가 손상되었는지 오류검출하는데 쓰이는 값입니다. 전달 할 정보를 7비트 단위로 만들고 이후 마지막 한 비트를 패리티 비트로 덧붙여서 8비트를 만듭니다. 이때 홀수 패리티 비트라고 할 경우, 패리티 비트가 포함되어 있는 8비트에서 1이 홀수개수가 되게끔 마지막에 덧붙여지는 패리티 비트 값이 0 또는 1이 됩니다. 반대로 짝수 패리티 비트일 경우 1이 짝수 개수가 되게끔 만듭니다. 위의 그림을 참고하시면 이해하기 쉽습니다. 다시 키 생성함수에서의 패리티 비트 제거로 돌아오면 8비트당 하나씩 존재하는 패리티 비트를 제거함으로 입력받은 64비트의 키 값은 56비트가 됩니다.

 

 

 

2.2.2. Shift

 

Logical Left Shift

 

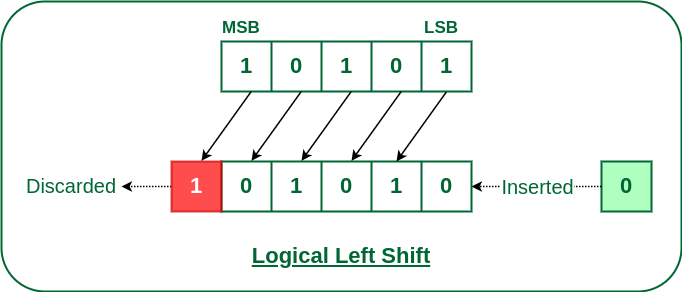
쉬프트 연산(Shift)은 쉽게 말해서 특정 비트 수 만큼 왼쪽이나 오른쪽으로 방향을 정해서 민다고 생각하시면 됩니다. 밀면 사라지는 비트 개수 만큼 끝부분에 0을 붙여줍니다. 위의 그림은 1비트만큼 왼쪽으로 쉬프트 연산을 한 그림입니다. 왼쪽으로 1비트만큼씩 밀면 가장 왼쪽에 위치한 1비트는 제거가 됩니다. 이후 비어있는 비트 개수만큼 0을 붙여줍니다. 일반적인 쉬프트 연산은 위의 그림과 같이 0을 붙여주지만 데이터의 손실이 일어납니다.

 

Circular Left Shift

 

Circular Right Shift

 

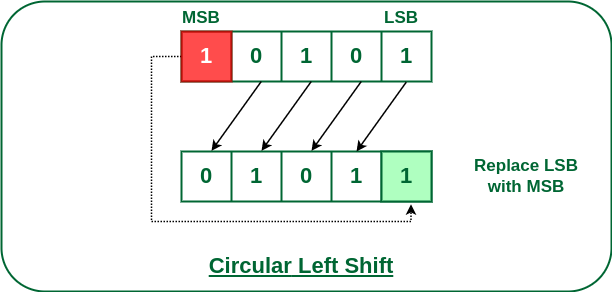
키 생성 함수에서 쓰이는 쉬프트 연산은 순환 쉬프트 연산이 쓰입니다. 앞에서 살펴봤던 쉬프트 연산에서 끝에 0을 붙여줘서 데이터의 손실이 발생했던거와 달리 0대신 앞부분의 비트 값들을 붙여주어서 데이터의 손실이 발생하지 않으며 이름대로 순환하는 형태입니다. 키 생성함수에서는 패리티 비트 제거 이후 28비트씩 절반으로 나누고 각각에 왼쪽 방향으로 순환 쉬프트 연산을 합니다. 키 생성 함수 그림에서 보이는 것 처럼 1, 2, 9, 16 라운드만 1비트씩 쉬프트 연산을 하고 그 외에 라운드는 2비트씩 쉬프트 연산을 합니다.

 

 

 

2.2.3. Compression P-box

 

Compression P-box

 

축소 순열(Compression P-box)를 통해 제거되는 값들은 다음과 같이 9, 18, 22, 25, 35, 38, 43, 54번째 비트들입니다. 불규칙적으로 제거됌을 알 수 있습니다. 따라서 28비트씩 각각 쉬프트 연산을 한 후 56비트가 축소 순열을 통해 48비트가 됌을 알 수 있습니다. (그림의 58비트는 오타로 보입니다.)

 

 

 

2.3 S-box

 

키 생성 함수에 대해 다 알아보았으므로 다시 라운드함수의 과정으로 돌아옵니다. 확장 순열을 거친 값과 키 생성함수를 통해 생성된 키 값이 서로 xor 연산을 하고 결과 값이 S-box로 입력됩니다. S-box는 입력되는 48비트를 32비트로 출력해줍니다. 먼저 입력되는 48비트의 값을 6비트씩 8그룹으로 나눕니다. 이후 6비트에서 맨 앞과 끝 비트가 행(row)를 결정하는 수가 되고, 중간의 4비트가 열(column)을 결정하는 수가 됩니다. 6비트가 8그룹이 있으므로 한 그룹당 행과 열이 정해져 있고 8개가 있습니다. 이것을 4비트안에 표현이 가능한 값들로 채워진 table에서 행과 열로 찾으면 4x8=32이므로 32비트가 출력이 됩니다. 참고하는 table은 그룹마다 달라서 8개의 table이 있습니다. 글로 보면 복잡하게 느껴지므로 아래의 그림을 참고 합니다.

 

S-box process

 

S1 ~ S8 box table

 

 

 

 

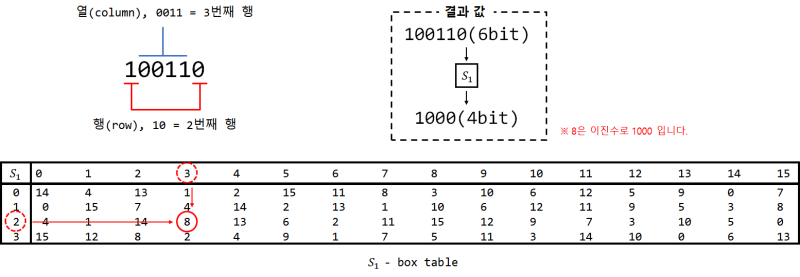
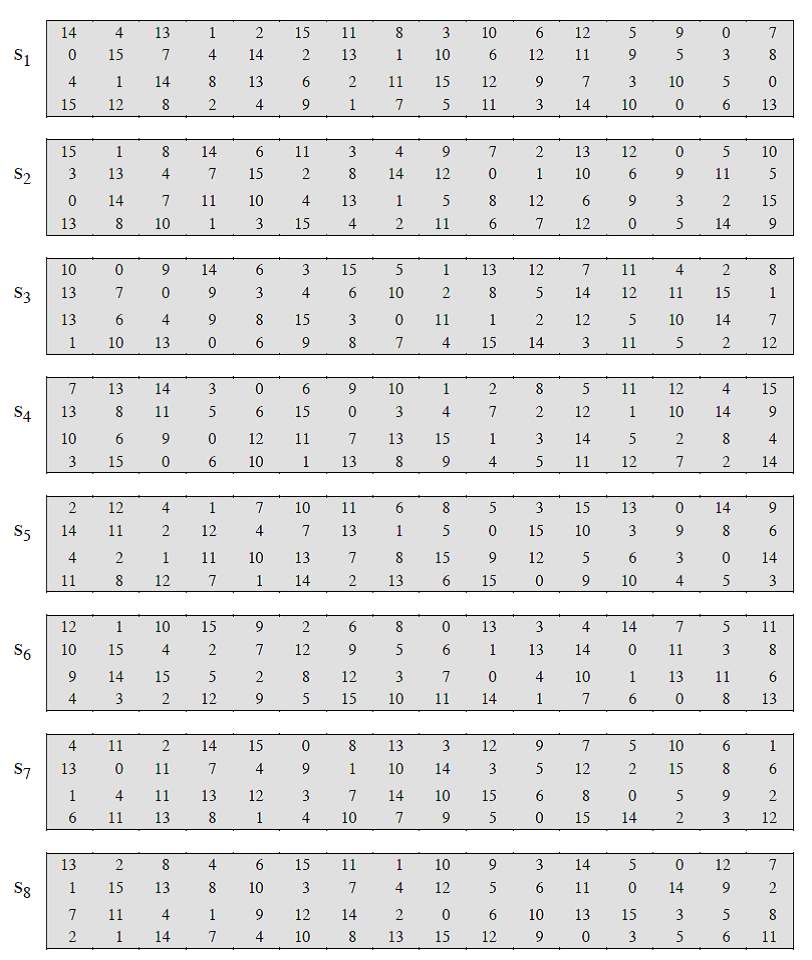
*** DES algorithm Review

 

DES algorithm (1)

 

DES algorithm (2)

 

Round function

 

Key scheduling

 

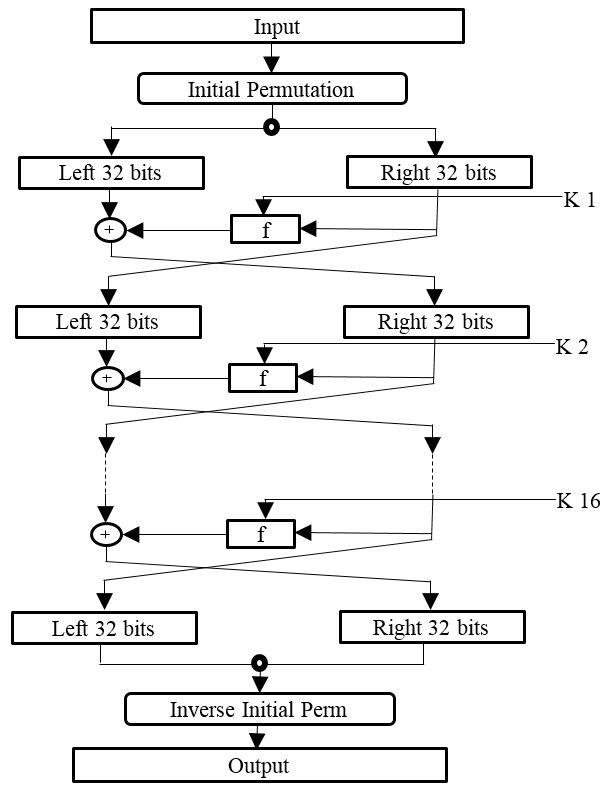
위의 전체적인 과정의 그림들을 다시 보면 DES를 거시적으로 이해하는데 도움이 됩니다 :)